I buchi neri. Una scoperta che ha radici nel settecento

Rendering del buco nero M87* (vedi fondo pagina per dettagli e per la 1a immagine diffusa) 
Credit: NASA

Alla domanda "chi ha proposto per primo l'idea di buco nero?" i primi nomi che verrebbero in mente sarebbero Albert Einstein, Stephen Hawking, Karl Schwarzschild o John Wheeler, che nel 1967, fu il primo ad usare il termine Black Hole durante una conferenza (NASA GISS), stufo di dovere ripetere "gravitationally completely collapsed object". 

Sebbene questi scienziati abbiano avuto un enorme impatto sull'astrofisica dei buchi neri, l'idea di un forte campo gravitazionale che altera la luce risale a molto prima, risale alla fine del '700 ad opera di un prete e professore di geologia dell'università di Cambridge di nome John Michell. 

Da sinistra Mitchell, LaPlace e Wheeler (credit: blackholecam)

Poco noto ai più ma considerato oggi il padre della moderna sismologia, e molto altro tra cui la descrizione teorica di quelle che chiamò Dark Stars, oggetti planetari in cui la velocità di fuga supera la velocità della luce.

L'ipotesi risale al 1783 quando Mitchell era già in pensione e faceva il rettore della chiesa di St. Michael a Thornill nello Yorkshire e (a tempo perso ...) dava sfogo alla sua inesauribile curiosità scientifica. 

L'articolo in cui esponeva le sue conclusioni apparve su The philosophical transactions nel 1784, una data non così lontana dall'essere temporalmente mediana tra la teoria della gravitazione universale di Newton e la teoria della relatività speciale di Einstein. 

In quel periodo Michell stava cercando di determinare un metodo per misurare la distanza e la luminosità delle stelle, usando come elementi di partenza le teorie della luce e della gravità. 

Il reverendo partiva dall'idea che la luce fosse costituita da una particella (un argomento estremamente dibattuto all'epoca) e che quindi la gravità potesse agire sulle particelle di luce nello stesso modo in cui agiva su tutti gli oggetti. 

Data l'incontrovertibile esistenza della gravità Michell cercò di calcolare la "velocità per raggiungere l'infinito", cioè la velocità di fuga, sulla Terra e nel Sole. Il ragionamento lo portò a considerare che se si spingeva la massa oltre un certo valore anche la forza di gravità sarebbe aumentata e con essa la velocità di fuga finché avrebbe raggiunto e superato la velocità della luce e a quel punto l'oggetto sarebbe apparso del tutto nero.

Nota. Una ipotesi formulata quando ancora non si aveva alcuna idea della reale velocità reale (sebbene nel 1676 il danese Ole Roemer provò che aveva un valore finito) e tantomeno che, come Einstein poi dimostrò, tale valore rappresentava un limite invalicabile e che nessun oggetto di massa poteva, per definizione, raggiungere. Alcuni presupposti di Mitchell (come la deduzione della velocità della luce ) non erano corrette ma qui importa il ragionamento con cui dedusse potessero esistere stelle nere invisibili agli occhi degli astronomi. Qui lui propose che se la stella nera avesse una compagna luminosa quest'ultima avrebbe fornito indizi sulla esistenza della prima; un sistema oggi ben noto quando si studiano sistemi binari in cui una stella è una stella di neutroni o un buco nero.

Una idea molto simile fu proposta nel 1796 dal matematico francese Pierre-Simon Laplace, che parlò di "corpo invisibile". Vero che la proposta fu di 10 anni successiva a quella di Mitchell ma il consensus attuale è che Laplace abbia sviluppato in completa autonomia questa teoria, fatto supportato dalla quasi totale assenza di comunicazione (non solo scientifica) tra Francia e Inghilterra in quel periodo di travaglio rivoluzionario. 

E' intellettualmente divertente ripetere oggi il processo matematico che portò Mitchell al concetto di stelle nere. 

Punto di partenza è la legge gravitazionale di Newton con la quale si può dedurre la velocità di fuga che è la condizione per cui l'energia cinetica pareggia l'energia potenziale gravitazionale.

Invece di risolvere per la velocità (come fatto nel precedente articolo), seguiamo Mitchell, cioè calcoliamo il raggio di un oggetto con massa M affinché abbia una velocità di fuga uguale alla velocità della luce (per cui sostituiamo Vf con c).

Eliminiamo per prima cosa la radice quadrata moltiplicando tutto al quadrato e moltiplichiamo entrambi i lati dell'equazione per R diviso "c" al quadrato, risolvendo poi per il raggio.

 

nota. "r" è da intendere in maiuscolo come nelle equazioni sopra (mio errore digitazione)

Ovvero, un corpo di massa M ha una velocità di fuga pari alla velocità della luce quando il suo raggio r è uguale a 2GM diviso C al quadrato. 

Da qui è immediato calcolare la dimensione che dovrebbero avere la Terra e il Sole affinché la velocità di fuga alla superficie sia uguale a quella della luce: 8,87 millimetri e 2,95 km, rispettivamente.

Piccoli? Le stelle di neutroni (da cui la recente conferma dell'esistenza delle onde gravitazionali) hanno un diametro inferiore all'isola di Manhattan (ca. 20 km)

In queste condizioni il Sole apparirebbe scuro dato che nessuna "particella di luce" (che noi oggi chiamiamo fotone) potrebbe fuggire da esso. Questo fenomeno, che nella fisica odierna rappresenta il caso più semplice di buco nero ("buchi neri di Schwarzschild ) fu previsto con il solo ausilio della fisica classica newtoniana.

Chiaramente Mitchell non poteva concepire l'idea di una densità di massa tale da giustificare stelle mignon, per cui ipotizzò una massa "sufficiente" allocata in stelle con raggio 500 volte quello solare in modo da allocare una massa sufficiente. Il risultato cambia poco data la predizione di stelle da cui è impossibile che la luce sfugga. 

Oggi si sa che mentre enormi masse (pari a miliardi di stelle solari) possono localizzarsi in buchi neri grandi tipo quelli nel centro galattico, la dimensione massima che può raggiungere una stella è vincolata a limiti precisi oltre i quali non ci potrà essere energia prodotta sufficiente per sostenere la massa soprastante. Ad oggi le stelle più grosse hanno raggio record di 2 mila volte quello del Sole.

L'equazione sviluppata da Mitchell sarebbe ricomparsa secoli dopo nella relatività generale di Einstein come soluzione di alcune equazioni e per spiegare l'orizzonte degli eventi (al posto di "R" si ha "REH" ad indicare il raggio della sfera che descrive l'orizzonte degli eventi - OE). Per il resto l'equazione predittiva delle Dark Stars di Mitchell è esattamente identica a quella ricavata da Einstein. Gli "oggetti" previsti sono invero diversi: per Mitchell era una stella con una propria "superficie" mentre oggi l'OE indica il punto oltre il quale si ha un collasso continuo, quindi impossibile avere una qualsivoglia idea di superficie.

Notevole quanto la matematica permetta di ottenere risultati talmente avanti nel tempo da non potere essere compresi ma solo "accettati", fino allo sviluppo di teorie adeguate. 

Nota. L'utilizzo della fisica newtoniana è sufficiente fintanto ci si trova in situazioni in cui la gravità è "debole", evidente quando la velocità di fuga calcolata è una mera frazione della velocità della luce. Condizioni che si trovano quando si mette in orbita un satellite o si calcola la traiettoria per andare sulla Luna e tornare (la velocità di fuga dalla Terra è 11,2 km/sec, circa 27 mila volte minore di "c". L'accurata predizione di quanto avviene con gravità tali da causare velocità di fuga intorno al 10% di "c" necessitano delle equazioni della teoria generale della relatività.

Fonte

-  harvard.edu

***Note finali***

La prima immagine di M87* risale ad aprile 2019, qui di seguito in formato GIF che è di fatto un time lapse di 8 anni

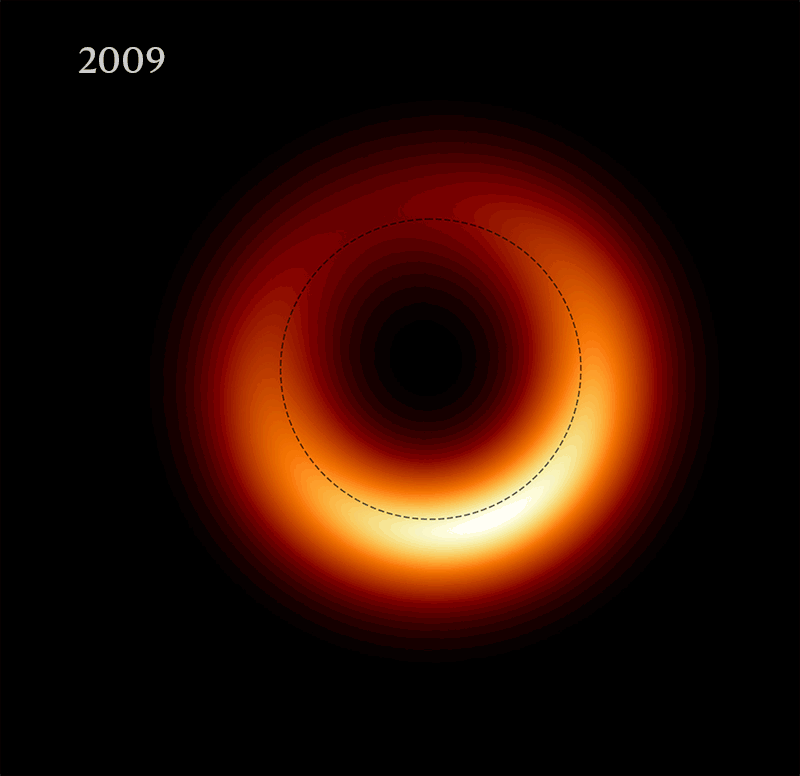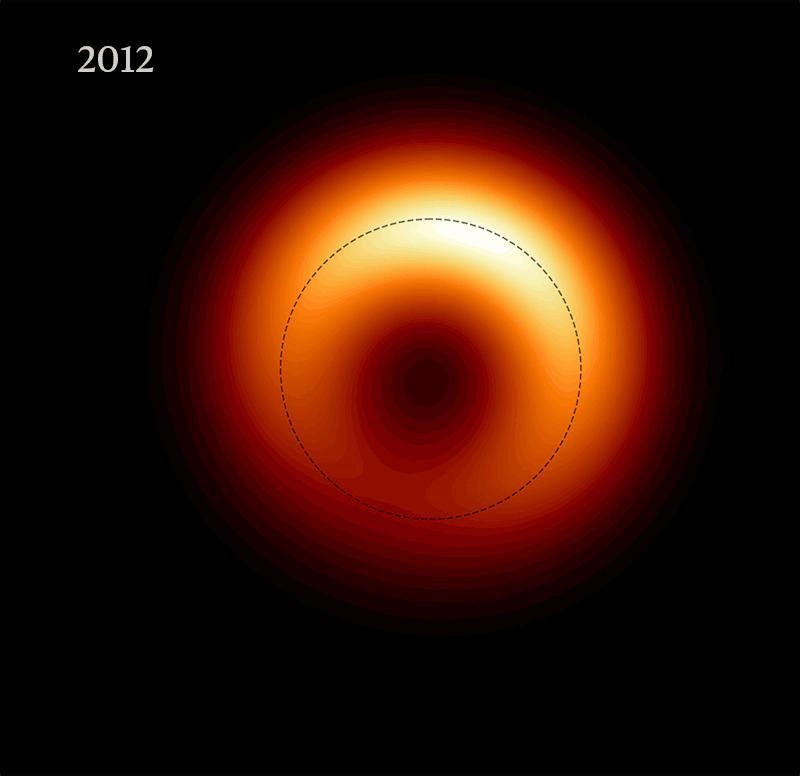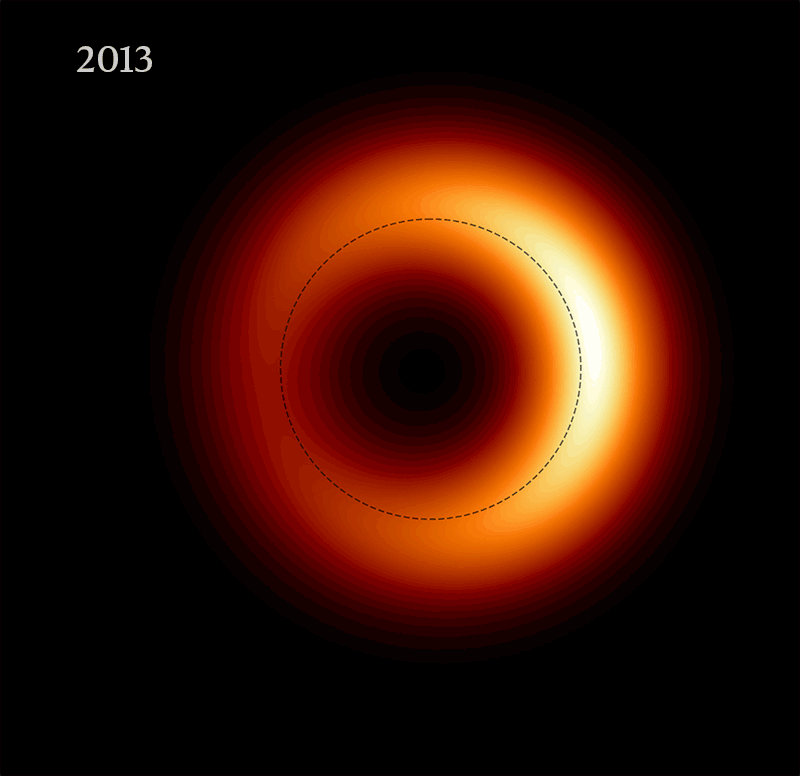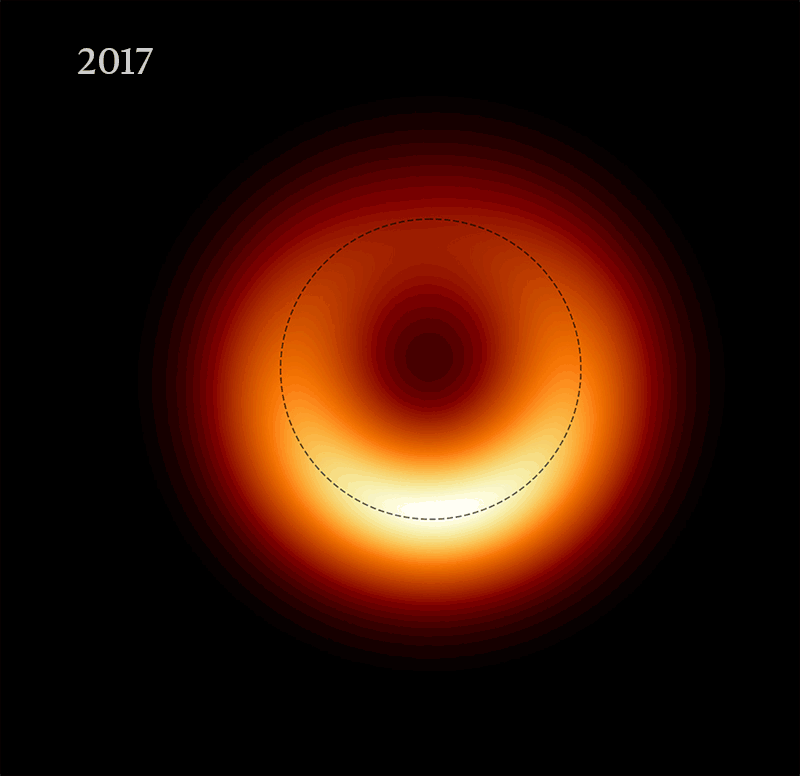Credit: Event Horizon Telescope Collaboration; gif compiled by Nature

Una immagine arricchita a fine marzo 2021 con i dettagli del campo magnetico

Immagine del buco nero al centro della galassia M87 in luce polarizzata. Le linee indicano l’orientazione della polarizzazione, legata al campo magnetico che circonda l’ombra del buco nero. Image Credit: Eht Collaboration.
Testo: INAF

Descrizione video dell'immagine precedente (all credit to youtube/INAF)

Di seguito i dettagli dell'immagine in apertura

Per dettagli vedi il sito della NASA e una spiegazione ottica del fenomeno QUI.

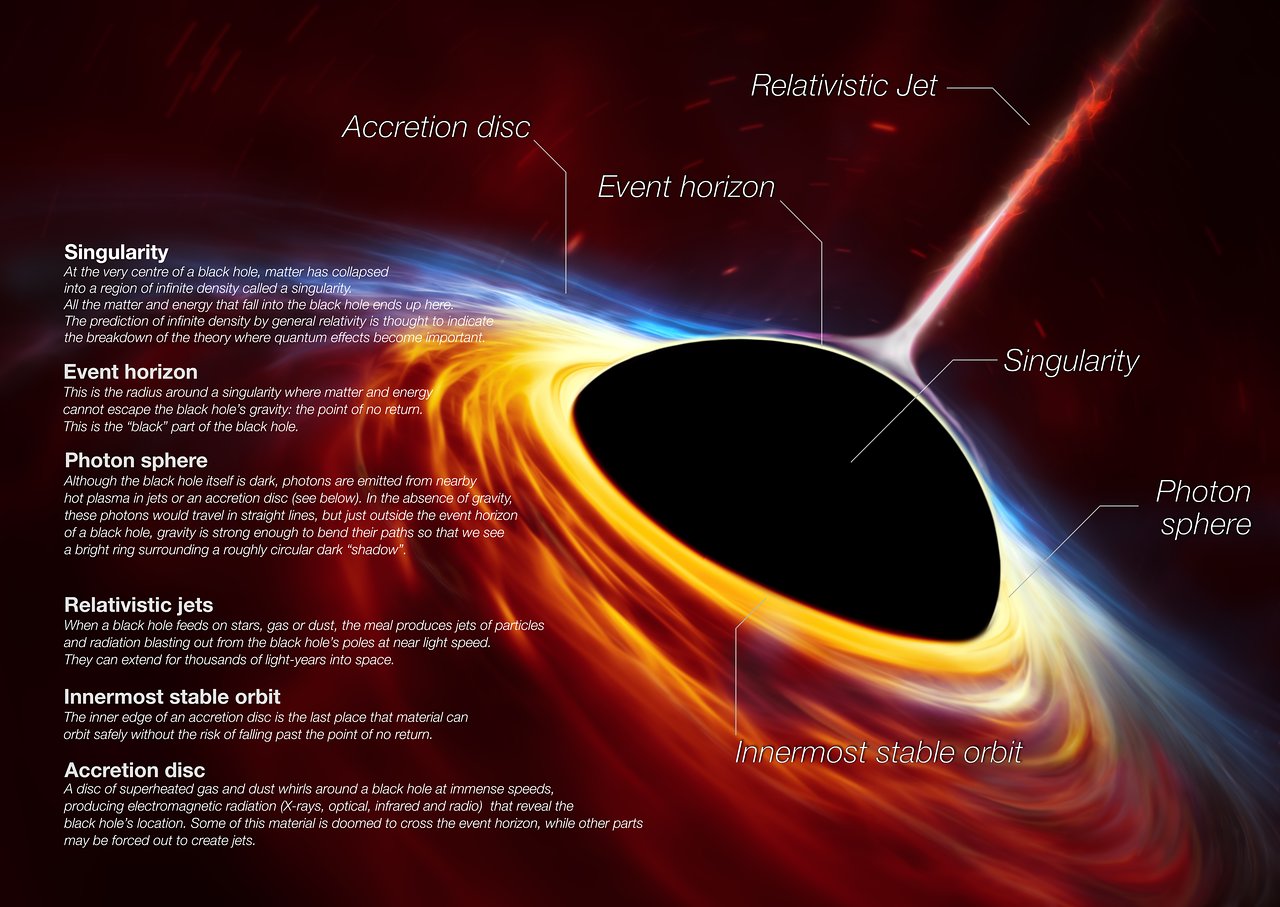Credit: ESO

Altri dettagli sul perché lo vediamo in un certo modo (image credit: Nature)

Articolo successivo sul tema --> Virtualizzazione di 2 buchi neri supermassicci.

Aggiornamenti.

Nel 2021 è stata pubblicata l'immagine di anelli intorno al buco nero V404 Cygni.

A maggio 2022 si è ottenuta l'immagine di Sgr A*.